Predicting Stock Prices using classical machine Learning (Time Series #2)

In this post/Jupyter Notebook we’ll look at stocks, forecasting and predictions using classical machine learning (sklearn) approaches.
machine-learning
timeseries
workshop
Author

Hampus Londögård

Published

March 12, 2022

Open In Colab

[CA]: Time Series #2 - Predicting Stock Prices (Time Series) using classical Machine Learning

CA=Competence Afternoon

To learn more about Time Series and how one can analyze them please view the other parts,

  1. Part One - Decomposing & Working with Time Series (theoretical) (Open In Colab)
  2. Part Two - Predicting Stock Prices (Time Series) using classical Machine Learning (Open In Colab)
  3. Part Three -Forecasting Cryptocurrency Prices (Time Series) using Deep Learning (PyTorch, Tensorflow/Keras & darts) (Open In Colab)

Predicting Time Series 📈

Today we will move from learning how to analyze Time Series to actually predicting them using simple models and data.

We’ll be predicting Stocks from the top tech companies like Apple & Google.
In part #3 we’ll move back to the crypto world!

To be able to predict the data we must understand it and we’ll make a minor analysis.

Installation & Imports

Feel free to ignore the cells and simply run them, the lazy style 🥱

Installing the important libraries…

from IPython.display import clear_output
!pip install -U pandas_datareader
!pip install plotly
!pip install matplotlib==3.1.3

clear_output()

And importing them…

import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
import numpy as np  # linear algebra
import pandas_datareader as pdr
import seaborn as sns

from datetime import datetime

Minor Analysis

df = pdr.get_data_yahoo(['AAPL', 'GOOGL', 'AMZN', 'MSFT', 'GE'])
df.head()
Attributes Adj Close Close ... Open Volume
Symbols AAPL GOOGL AMZN MSFT GE AAPL GOOGL AMZN MSFT GE ... AAPL GOOGL AMZN MSFT GE AAPL GOOGL AMZN MSFT GE
Date
2017-03-13 32.856758 864.580017 854.590027 60.405796 214.961868 34.799999 864.580017 854.590027 64.709999 229.692307 ... 34.712502 860.830017 851.770020 65.010002 232.538467 69686800.0 1166600.0 1909700.0 20100000.0 3924414.0
2017-03-14 32.807198 865.909973 852.530029 60.125748 212.658188 34.747501 865.909973 852.530029 64.410004 227.230774 ... 34.825001 863.750000 853.549988 64.529999 228.923080 61236400.0 1061700.0 2130600.0 14280200.0 2964208.0
2017-03-15 33.154182 868.390015 852.969971 60.443142 214.241943 35.115002 868.390015 852.969971 64.750000 228.923080 ... 34.852501 867.940002 854.330017 64.550003 227.307693 102767200.0 1332900.0 2562200.0 24833800.0 3268564.0
2017-03-16 33.208458 870.000000 853.419983 60.340446 214.169952 35.172501 870.000000 853.419983 64.639999 228.846161 ... 35.180000 870.530029 855.299988 64.750000 229.230774 76928000.0 1104500.0 1842300.0 20674300.0 2756910.0
2017-03-17 33.043243 872.369995 852.309998 60.555161 215.105865 34.997501 872.369995 852.309998 64.870003 229.846161 ... 35.250000 873.679993 853.489990 64.910004 229.615387 175540000.0 1868300.0 3384400.0 49219700.0 5673070.0

5 rows × 30 columns

Looks fine, but how much data did we download?
We can view the .index which is a DateTimeIndex and figure out how it stretches.

df.index[0],df.index[-1]
(Timestamp('2017-03-13 00:00:00'), Timestamp('2022-03-11 00:00:00'))

Hmm, 5 years, that should be enough to find some kind of patterns.
Now let us analyze this data further by looking at if the stocks correlate somehow! 🤠

N.B. this analysis was first done by Heidi Mach, it’s something I would never have done myself. Really cool results incoming!

df['Adj Close'].corr().style.background_gradient(cmap="Blues")
Symbols AAPL GOOGL AMZN MSFT GE
Symbols          
AAPL 1.000000 0.951499 0.935116 0.978268 -0.283789
GOOGL 0.951499 1.000000 0.866575 0.960291 -0.192826
AMZN 0.935116 0.866575 1.000000 0.944313 -0.499768
MSFT 0.978268 0.960291 0.944313 1.000000 -0.374930
GE -0.283789 -0.192826 -0.499768 -0.374930 1.000000

Holy macaron, that’s a lot more correlated data than I expected! 🙀

The seaborn library has a function called pairplot which plots this correlation, but using the points which is visually interesting in comparison to simply seeing the table above.

df = df['Adj Close']
df = df.drop(columns="GE")
sns.pairplot(df)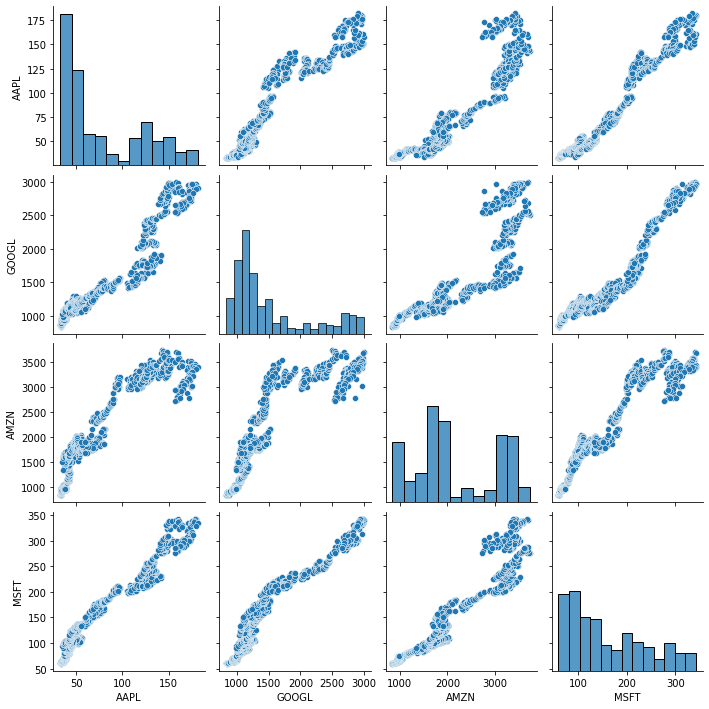

Does this in fact mean what that we can predict prices of a stock based on their competition? The correlation does suggest so.

Let’s try it!

First we’ll try using a LinearRegression which simply said fits a line to be as close to all points as possible.

linear regression wikipedia > Source: Wikipedia.org

First we import LinearRegression through scikit-learn and then we add train_test_split which allows us to split our data into a training and testing dataset.

Whenever you test your Machine Learning or Deep Learning Models you never want to test it on data that it has trained on, as you might’ve overfitted the data and have a really good result until you see new data points.

The end-goal of a model is to generalize a problem and find the local minima which optimizes the funtion for the data points. By only looking at the same data we can’t be sure we generalized correctly.

And the code 👩‍💻

from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import r2_score, mean_absolute_error

non_google_df = df.drop(columns="GOOGL")
X_train, X_valid, y_train, y_valid = train_test_split(non_google_df, df['GOOGL'], test_size=0.2)

clf = LinearRegression()

We got our data divided into valid and train, we got a regression model in our clf.

Let us predict the data and view our r2_score and mean_absolute_error.

💡
r2_score: (coefficient of determination) regression score function.
Best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of y, disregarding the input features, would get a score of 0.0.

mean_absolute_error: Mean absolute error regression loss.

clf.fit(X_train, y_train)
preds = clf.predict(X_valid)

r2_score(y_valid, preds), mean_absolute_error(y_valid, preds)
(0.9495278677136834, 120.88640110098741)

\(R^2 = 93 \%\) 🥳

That’s actually not bad at all, the mean_absolute_error being 129.7 is not very telling. Either we have to view the data to understand the magnituide, or we can apply MAPE which is the Mean Absolute Percentage Error.

Not sure if I’m lazy or simply want to show you the other function 🤔, but I’ll use MAPE!

from sklearn.metrics import mean_absolute_percentage_error

mean_absolute_percentage_error(y_valid, preds)
0.07891126366405354

\(< 9\%\)
Pretty acceptable considering we have not done anything except deliver data to one of the simplest models that exists!

Let’s show this visually!

import plotly.express as px

px.line(y=[y_valid, preds])
Show Plotly Chart (code cell only visible in active notebook)

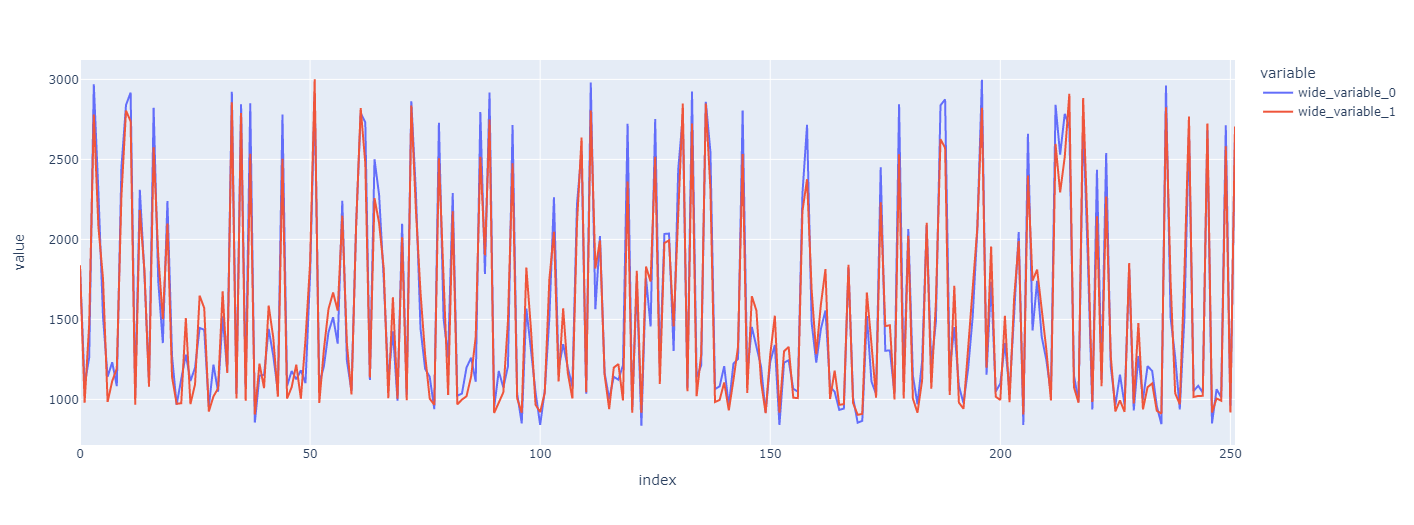
Looks pretty good, but it is very messy… Something is off right?

The index is not a DateTimeIndex anymore because we shuffled the data in train_test_split – a big difference is thereby applied.

y_valid.plot()

y_valid.plot(legend="Valid")
pd.Series(preds, index=y_valid.index).plot(legend="Pred")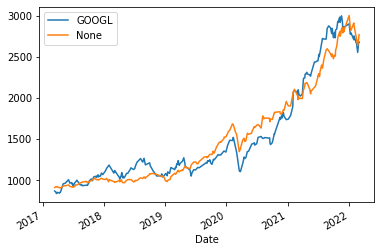

Looks pretty fly, but can we take it further?
…yes we can! 😎

I see a few options, the two first being:

  1. Scaling the data as errors at the end are larger than in the beggining based on stocks rising.
  2. LinearRegression is a very simple yet efficient model that we can try to replace.

Let’s start with the second point, scikit-learn has a multitude of regression-models, one being RandomForestRegressor that’s pretty strong.

from sklearn.ensemble import RandomForestRegressor

clf = RandomForestRegressor()
clf.fit(X_train, y_train)

preds = clf.predict(X_valid)
r2_score(y_valid, preds), mean_absolute_percentage_error(y_valid, preds)
(0.9963567300739637, 0.016329169939121136)

😲\(R^2 >99\%\)

That’s actually crazy. And MAPE is not even 2%.

Let’s view it!

y_valid.plot(legend="Valid")
pd.Series(preds, index=y_valid.index).plot(legend="Pred")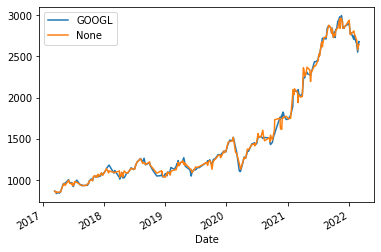

That’s an incredibly fitted curve.

How is this possible?
1. We most likely overfit the data.
2. We are looking at AMZN, AAPL and more data that is highly correlated during the same day as the one we wish to predict. - In the end this is a useless task, if we know the prices of today we’d also know GOOGL’s prices! 3. We’re using shuffled data, meaning that in a way we’ve seen the future and past values surrounding the predicted one. This is a regression problem and not really a forecasting problem, which is simpler than forecasting.

Impressive nontheless
Even as I’m aware of all the drawbacks I’m thouroughly impresed by the results we’re seeing.

Making it more interesting
We should make use of the previous days data to make sure we are not “cheating”.

Let’s get on it! 🎯

We’ll be able to move, or shift, the data using ˋpd.DataFrame.shiftˋ which shifts the data either forwad (\(+X\)) or backwards (\(-X\)).

And while we’re at it, let’s group this up into a function.

ℹ️
pd.DataFrame.shift: Shift index by desired number of periods with an optional time freq.

def fit_validate_plot(X_train, X_valid, y_train, y_valid):
  clf = RandomForestRegressor()
  clf.fit(X_train, y_train)

  preds = clf.predict(X_valid)
  pd.DataFrame({'Valid': y_valid, 'Preds': preds}, index=y_valid.index).plot()
  
  print(f"""
  $R^2$: {r2_score(y_valid, preds)}
  MAPE: {mean_absolute_percentage_error(y_valid, preds)}
  MAE: {mean_absolute_error(y_valid, preds)}
  """)

And making use of it will now be easy! 😍
Refactoring and abstractions are incredibly important.

X_train, X_valid, y_train, y_valid = train_test_split(df.drop(columns="GOOGL").shift(1).iloc[1:], df['GOOGL'].iloc[1:], test_size=0.2)

fit_validate_plot(X_train, X_valid, y_train, y_valid)

  $R^2$: 0.993020486528333
  MAPE: 0.022105878493046974
  MAE: 32.473562898181726

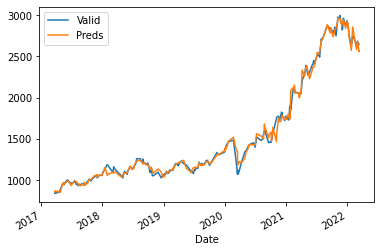
🤯 this is crazy impressive!

We made the task at hands legit by only using historical data of GOOGL’s competitors. The \(R^2\) and MAPE is incredible.

It’d be interesting to investigate how badly we overfit the data, but that’s for another day.

And how about if we don’t shuffle the data? E.g. we do an actual forecast and not regression!

X_train, X_valid, y_train, y_valid = train_test_split(df.drop(columns="GOOGL").shift(1).iloc[1:], df['GOOGL'].iloc[1:], test_size=0.2, shuffle=False)

fit_validate_plot(X_train, X_valid, y_train, y_valid)

  $R^2$: -7.266054917956771
  MAPE: 0.24703039286319634
  MAE: 675.8480126274956

🤯😭

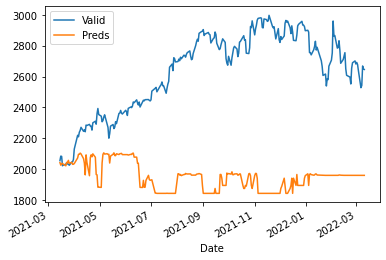
What are we seeing and why?
Regression algorithms/models try to fit a line to multiple points and it should be able to guess what point the data has depending on its features. In our case the regression algorithm has never seen data as high as above y_train.max(), which means it can’t guess the data.

Don’t trust me? Simply validate by looking at the chart 👆.

What’s one way to fix this? Scaling
How will we try to achieve this practically? LogReturn

💡 You can also take the %-difference, which according to Taylors Theorem will approximate the LogReturn.

def log_return(x: pd.DataFrame) -> pd.DataFrame:
  return x.apply(lambda x: np.log(x/x.shift(1))).dropna()

log_return(df).head()
Symbols AAPL GOOGL AMZN MSFT
Date
2017-03-14 -0.001510 0.001537 -0.002413 -0.004647
2017-03-15 0.010521 0.002860 0.000516 0.005265
2017-03-16 0.001636 0.001852 0.000527 -0.001700
2017-03-17 -0.004987 0.002720 -0.001301 0.003552
2017-03-20 0.010446 -0.005126 0.005453 0.000925 
df_lr = log_return(df)
X_train, X_valid, y_train, y_valid = train_test_split(df_lr.drop(columns="GOOGL").shift(1).iloc[1:], df_lr['GOOGL'].iloc[1:], test_size=0.2, shuffle=False)

fit_validate_plot(X_train, X_valid, y_train, y_valid)

  $R^2$: -0.13772674709610588
  MAPE: 3.1419364874467086
  MAE: 0.01222694796828883

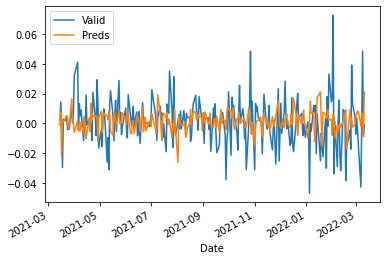
Most certainly not perfect… Forecasting seems harder than expected based on our initial results…
And that’s really because we weren’t forecasting before, we were solving a regression-problem

Perhaps we need to use more data than simply the previous day?

Predicting Based on historical performance

We might predict based on historical performance.

df.head()
Symbols AAPL GOOGL AMZN MSFT
Date
2017-03-13 32.856758 864.580017 854.590027 60.405796
2017-03-14 32.807198 865.909973 852.530029 60.125748
2017-03-15 33.154182 868.390015 852.969971 60.443142
2017-03-16 33.208458 870.000000 853.419983 60.340446
2017-03-17 33.043243 872.369995 852.309998 60.555161 
df = df[['GOOGL']]
df.head()
Symbols GOOGL
Date
2017-03-13 864.580017
2017-03-14 865.909973
2017-03-15 868.390015
2017-03-16 870.000000
2017-03-17 872.369995

✅ Only Google Data
❌ Historical Data

So what should we do? One way to solve this is to use shift multiple times.

def build_history(df: pd.DataFrame, num_back: int) -> pd.DataFrame:
  for i in range(num_back):
    df.loc[:, f"t_{i}"] = df['GOOGL'].shift(i + 1)
  
  return df

build_history(df, 3).head()
/usr/local/lib/python3.7/dist-packages/pandas/core/indexing.py:1667: SettingWithCopyWarning:


A value is trying to be set on a copy of a slice from a DataFrame.
Try using .loc[row_indexer,col_indexer] = value instead

See the caveats in the documentation: https://pandas.pydata.org/pandas-docs/stable/user_guide/indexing.html#returning-a-view-versus-a-copy
Symbols GOOGL t_0 t_1 t_2
Date
2017-03-13 864.580017 NaN NaN NaN
2017-03-14 865.909973 864.580017 NaN NaN
2017-03-15 868.390015 865.909973 864.580017 NaN
2017-03-16 870.000000 868.390015 865.909973 864.580017
2017-03-17 872.369995 870.000000 868.390015 865.909973

Notice how \(t_0\) is the previous value, \(t_1\) two steps back, and so on.
This is actually very memory intense as our data grows X times, one time per time step we build. In part #3 we’ll go through how one can solve this issue.

No we need to drop all places where we don’t have any history. That is easily achieved by dropping NaN.

ℹ️
pd.DataFrame.dropna: Remove missing values.
axis attribute tells if you wish to drop rows or columns based on NaN, default is row.

df = build_history(df, 7)
df = df.dropna()
df.head()
Symbols GOOGL t_0 t_1 t_2 t_3 t_4 t_5 t_6
Date
2017-03-22 849.799988 850.140015 867.909973 872.369995 870.000000 868.390015 865.909973 864.580017
2017-03-23 839.650024 849.799988 850.140015 867.909973 872.369995 870.000000 868.390015 865.909973
2017-03-24 835.140015 839.650024 849.799988 850.140015 867.909973 872.369995 870.000000 868.390015
2017-03-27 838.510010 835.140015 839.650024 849.799988 850.140015 867.909973 872.369995 870.000000
2017-03-28 840.630005 838.510010 835.140015 839.650024 849.799988 850.140015 867.909973 872.369995

LGTM ✅

Let’s scale our data and then make predictions.
As previously,

  1. Scale data
  2. Split data
  3. Fit data
  4. Predict data
  5. Validate
df_lr = log_return(df)
X_train, X_valid, y_train, y_valid = train_test_split(df_lr.iloc[:, 1:], df_lr['GOOGL'], test_size=0.2, shuffle=False)

fit_validate_plot(X_train, X_valid, y_train, y_valid)

  $R^2$: -0.12436497765470134
  MAPE: 2.020486730297106
  MAE: 0.011961155812517109

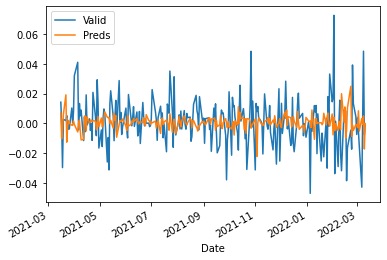
Not great, not awful. Some self-exercises:

  1. How would we do without scaling?
  2. How would we do without shuffling?
  3. Any other ideas? Try ’em out!
# Test your own ideas

If you didn’t try previously, try appling a rolling mean and rerun fit_validate_plot as this should reduce the “swings” and thereby be a little bit more predictable.

💡 pd.DataFrame.Rolling: Provide rolling window calculations.
In other words: We slide a window on our data and do calculations, in our case mean. This window includes window, min_periods, center & more attributes which impacts size of window, how large minimal window can be, and more.

Validating what rolling.mean() does to our data:

df['GOOGL_ROLLING'] = df['GOOGL'].rolling(3).mean()  # Rolling over 3 days mean
df[-100:].plot(y=['GOOGL', 'GOOGL_ROLLING'])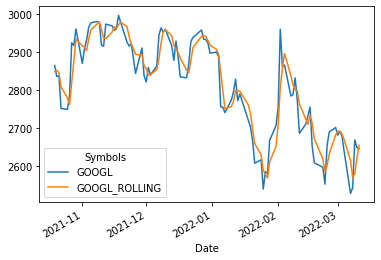

Zooming 🔍

df_last_months = df[df.index > datetime(2021, 6, 6)]

df_last_months.plot(y=['GOOGL', 'GOOGL_ROLLING'], backend='plotly')
Show Plotly Chart (code cell only visible in active notebook)

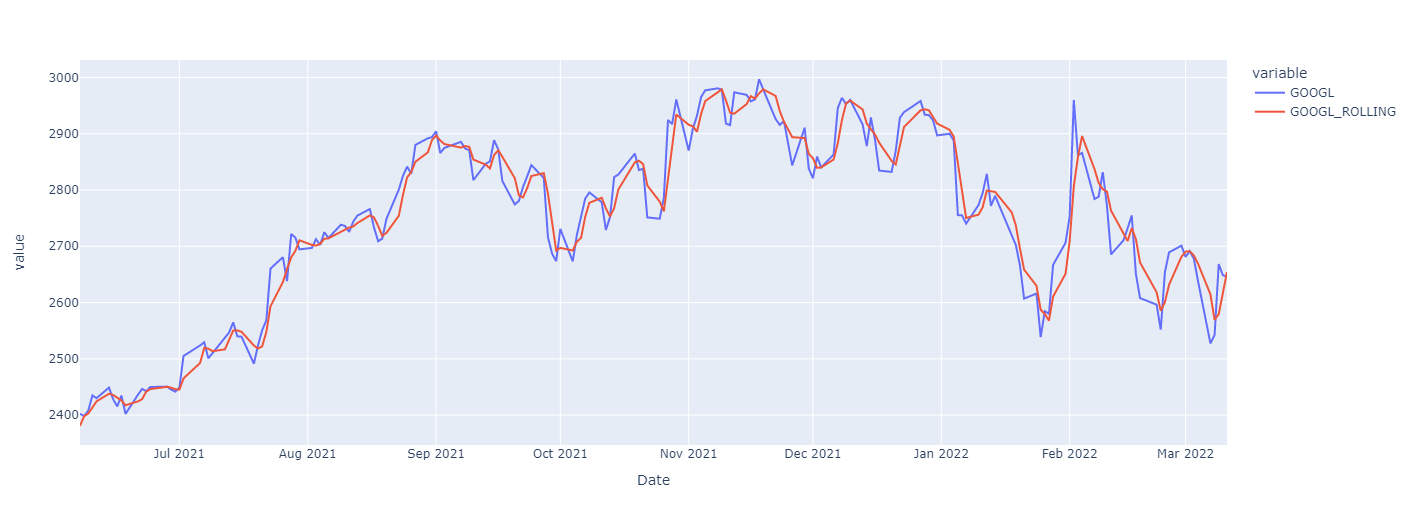
The curve is very similar, but different.

Self-exercise: Test applying different functions like min, max and expanding window size into more days.

And validating what this does to our prediction.

df_lr = df.pct_change().dropna().rolling(3).mean().dropna()
X_train, X_valid, y_train, y_valid = train_test_split(df_lr.iloc[:, 1:], df_lr['GOOGL'], test_size=0.2, shuffle=False)

fit_validate_plot(X_train, X_valid, y_train, y_valid)

  $R^2$: 0.8925898146393952
  MAPE: 0.7957020086330117
  MAE: 0.0020138783337579776

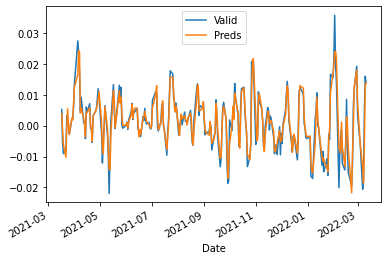
We’re back! 🥳

It’s not perfect, but we got something. And we can work with something. We can work with something… :)

Self-exercise: Validat how rolling would affect our non-history-based forecasting

Let’s reverse our transformation to see what we’d actually predict in the end.

y_rolling = df['GOOGL'].rolling(3).mean().dropna()
y_train_non_scaled, y_valid_non_scaled = train_test_split(y_rolling, test_size=0.2, shuffle=False)
clf = RandomForestRegressor()
clf.fit(X_train, y_train)
preds = clf.predict(X_valid)

preds = (preds + 1).cumprod() # Cummulative multiplication, first day + 1%, but then we got -1%, that's 1.01 * 0.99
preds = preds * y_train_non_scaled.iloc[-1] # Scaling it up based on the last training value

pd.DataFrame({'Preds': preds, 'Valid Rolling': y_valid_non_scaled[1:], 'Valid': df['GOOGL'].iloc[-len(preds):]}).plot(backend='plotly')
Show Plotly Chart (code cell only visible in active notebook)

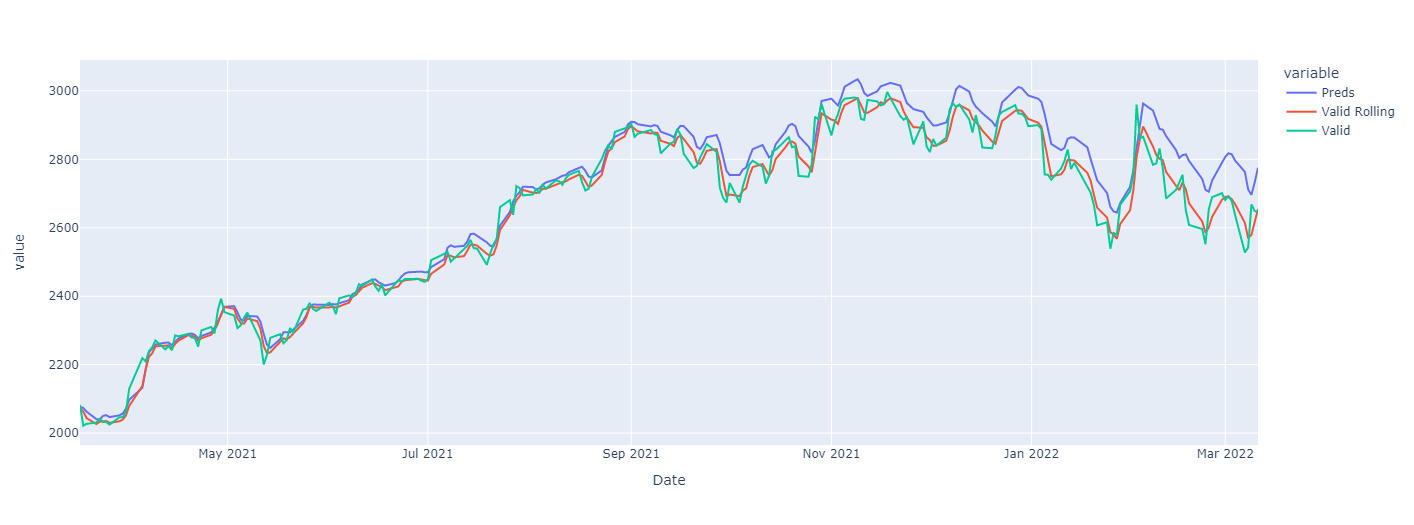
Seems as we’re a little low in our predictions, but the curve is followed after all.

What issues are left?

  1. We are not using an AutoRegressive model which might be interesting.
  • More about this in the next session
  1. We are not using the “better” models, e.g. Neural Networks or statistic-model for Time Series like ARIMA.

Personally I’m very pleased with the results and can’t wait to get started on part #3!

To learn more about Time Series and how one can analyze them please view the other parts,

  1. Part One - Decomposing & Working with Time Series (theoretical)
  2. Part Two - Predicting Stock Prices (Time Series) using classical Machine Learning
  3. Part Three -Forecasting Cryptocurrency Prices (Time Series) using Deep Learning (PyTorch, Tensorflow/Keras & darts)

Extra Self Exercises

  1. Try different window-sizes with rolling
  2. Try different length of history to predict new result on
  3. Test new architectures
  4. Find your own way to improve the results