[CA]: Time Series #1 - Decomposing & Working with Time Series

CA=Competence Afternoon

This CA is originally found on kaggle.com/lundet/.., as we entered a competition to predict cryptocurrency prices - G-Research Crypto Forecasting.

N.B. This blog/notebook is adapted into a Jupyter notebook that’s easier to replicate, that is we don’t use the Kaggle API + GBs of data that was required for said competition.

Part One - Decomposing & Working with Time Series (theoretical) ()
Part Two - Predicting Stock Prices (Time Series) using classical Machine Learning ()
Part Three -Forecasting Cryptocurrency Prices (Time Series) using Deep Learning (PyTorch, Tensorflow/Keras & darts) ()

Moving on to the content! 🤓

Time Series Concepts

Time Series has some important attributes that are unique compared to other data types such as Text, Image and Tabular.

Time Series can be decomposed into multiple other time series that together compose the decomposed one (composition baby!).

Trend	Seasonality	Combined

As shown above we can build a time series out of a Trend and Seasonality, that means we can also decompose the Combined into Trend and Seasonality.

This can be done in a few ways, mostly either through a additive or multiplicative decomposition.

Additive means that if we add Trend and Seasonality together we create Combined.
Multiplicative means that if we multiply Trend and Seasonality together we create Combined.

But these two are not enough to compose a full time series, usually we have noise too.

Noise	Trend+Seasonality+Noise

It seems we’re onto something. But still it’s not really how we usually see time series!

What else is left? Autocorrelation!

Autocorrelation is a correlation between two observation at different time steps, if values separated by an interval have an strong positive or negative correlation it’s indicated that past values influence the current value.

To keep it simple, if a time series is autocorrelated it’s new state has a correlation with a earlier step.

Autocorrelation	Trend+Autocorrelation

Trend+Seasonality+Autocorrelation	Trend+Seasonality+Autocorrelation+Noise

And there we go! 😎

We got a legit timeseries, pat yourself on your back and be proud. We did it.

Let’s get started with real data… 🧑‍💻

Installation & Importing

We need to have libraries which allows us to simplify operations and focus on the essential.

pandas is a DataFrame library that allows you to visualize, wrangle, and investigate data in different ways
numpy is a math library which is implemented in C and Fortran and combined with vectorized code it’s incredibly fast!
- This is key in Python as Python is a really slow language.
pandas_datareader gives us easy access to different data formats, directly in pandas
plotly gives your plots the next level interactivity that you’ve always wanted

from IPython.display import clear_output
!pip install -U pandas_datareader
!pip install plotly

clear_output()

And importing our libraries

import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
import numpy as np  # linear algebra
import pandas_datareader as pdr

from datetime import datetime

Reading Cryptocurrency Data

Using pandas_datareader we can query multiple API:s, and among them Yahoo.
Yahoo as a financial API that follows stocks, currencies, cryptocurrencies and much more!

Let’s see what we can do.

df = pdr.get_data_yahoo('BTC-USD', start=datetime(2020, 1, 1), end=datetime(2022, 1, 1))
df.head()

	High	Low	Open	Close	Volume	Adj Close
Date
2020-01-01	7254.330566	7174.944336	7194.892090	7200.174316	18565664997	7200.174316
2020-01-02	7212.155273	6935.270020	7202.551270	6985.470215	20802083465	6985.470215
2020-01-03	7413.715332	6914.996094	6984.428711	7344.884277	28111481032	7344.884277
2020-01-04	7427.385742	7309.514160	7345.375488	7410.656738	18444271275	7410.656738
2020-01-05	7544.497070	7400.535645	7410.451660	7411.317383	19725074095	7411.317383

The data seems great, but one should always validate it visually and programmatically.
How about plotting it first?

Plotting can be done in multiple ways, let’s start using the pandas way. 🐼

pandas/docs/plot
Make plots of Series or DataFrame.
Includes options like x, y, kind (e.g. line, bar or density) and much more.

df['Close'].plot()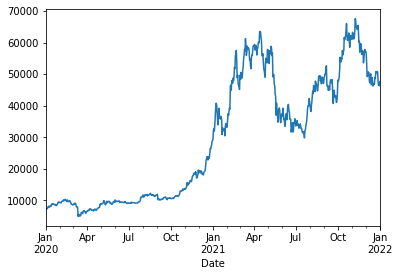

Let’s add some interactivity to this, and plot Low/High on top of that!
Super simple using plotly as the backend! 😎

df[['Close', 'High', 'Low']].plot(backend='plotly')

Show plotly chart (as it’s invisible in blog-mode)

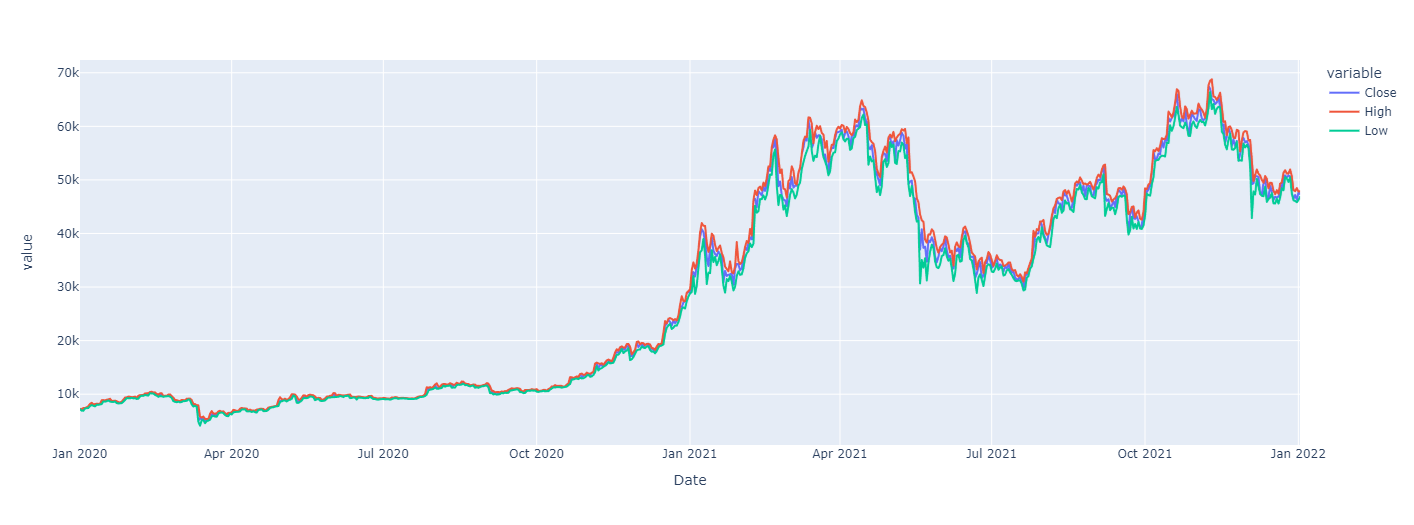
You can also plot a candle-stick chart by using

import plotly.graphical_objects as go

fig = go.Figure(data=[go.Candlestick(x=df.index,
                open=df['Open'],
                high=df['High'],
                low=df['Low'],
                close=df['Close'])])

The data does look nice, but we need to figure if there’s any issues in the data.
Graphs might be missing some values that are not clearly visible as there’s so much data. Our final data validation should always be programatical.

Data Validation

Validating that data makes sense and that there’s no errors is very important when you’re building models. Having outliers, errors and other things can lead to some really weird behaviour.

There’s a few tools we can use:

pd.DataFrame.isna:
Detect missing values. Return a boolean same-sized object indicating if the values are NA. NA values, such as None or numpy.NaN, gets mapped to True values.
💡The reverse, notna also exists.

df.isna().head()

	High	Low	Open	Close	Volume	Adj Close
Date
2020-01-01	False	False	False	False	False	False
2020-01-02	False	False	False	False	False	False
2020-01-03	False	False	False	False	False	False
2020-01-04	False	False	False	False	False	False
2020-01-05	False	False	False	False	False	False

Can we we make this more readable?
Yes! Using .any(), or even ‘cheating’ using .sum()

df.isna().any()

High         False
Low          False
Open         False
Close        False
Volume       False
Adj Close    False
dtype: bool

df.isna().any().any() # 👀

False

LGTM ✅

Next up: Validating that there’s no missing days

This can be done in multiple ways, but for now I choose to use .diff.

pd.DataFrame.diff: First discrete difference of element.
Bonus: Diff can also handle periods and axis arguments, period being how far to diff.

df.index.to_series().diff().dt.days.head()

Date
2020-01-01    NaN
2020-01-02    1.0
2020-01-03    1.0
2020-01-04    1.0
2020-01-05    1.0
Name: Date, dtype: float64

Ok, so we’ve got a series. Try to validate that no diff is greater than 1 day using a broadcasted/vectorized operation.

hint: pandas automatically broadcast operations by operator overloading, e.g. >, + etc

I think we can call quits on the validation part for now.

Let’s move on to different ways we can format the data, a common format is LogReturn.

Transforming Data

Because data is very different moving in time we wish to normalize the data somehow. This can be done in multiple ways, some common ways are:

pd.DataFrame.diff which takes the difference between x_1 and x_2

The negative aspect of this is that the difference is still not scaled

pd.DataFrame.pct_change which validates the % difference
LogReturn which is the logarithmic return between each time step (x_1, x_2, ..).
Apply a Scaler which scales the data somehow

Can be MinMaxScaler which scales Min and Max to (0,1) or (-1,1)
Can be a MeanScaler which scales the data to have a mean of 0.

… and more.

We’ll start of with LogReturn which is common in forecasting of stocks.

def log_return(series, periods=1):
    return np.log(series).diff(periods=periods)

df['LogReturn'] = log_return(df['Close'])
df['LogReturn'].head()

Date
2020-01-01         NaN
2020-01-02   -0.030273
2020-01-03    0.050172
2020-01-04    0.008915
2020-01-05    0.000089
Name: LogReturn, dtype: float64

Because .diff takes the diff with the next element you’ll end up with a NaN, as such we wish to remove the first element.

df = df[1:]
df['Close'].head()

Date
2020-01-02    6985.470215
2020-01-03    7344.884277
2020-01-04    7410.656738
2020-01-05    7411.317383
2020-01-06    7769.219238
Name: Close, dtype: float64

df['LogReturn'].plot()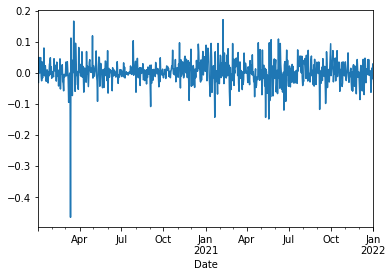

Looks nice.

For now we’ll leave it here and move on to looking at Correlation.

Data Analysis: Correlation

df = pdr.get_data_yahoo(['BTC-USD', 'ETH-USD'], start=datetime(2020, 1, 1), end=datetime(2022, 1, 1))
df.head()

Attributes	Adj Close		Close		High		Low		Open		Volume
Symbols	BTC-USD	ETH-USD	BTC-USD	ETH-USD	BTC-USD	ETH-USD	BTC-USD	ETH-USD	BTC-USD	ETH-USD	BTC-USD	ETH-USD
Date
2020-01-01	7200.174316	130.802002	7200.174316	130.802002	7254.330566	132.835358	7174.944336	129.198288	7194.892090	129.630661	18565664997	7935230330
2020-01-02	6985.470215	127.410179	6985.470215	127.410179	7212.155273	130.820038	6935.270020	126.954910	7202.551270	130.820038	20802083465	8032709256
2020-01-03	7344.884277	134.171707	7344.884277	134.171707	7413.715332	134.554016	6914.996094	126.490021	6984.428711	127.411263	28111481032	10476845358
2020-01-04	7410.656738	135.069366	7410.656738	135.069366	7427.385742	136.052719	7309.514160	133.040558	7345.375488	134.168518	18444271275	7430904515
2020-01-05	7411.317383	136.276779	7411.317383	136.276779	7544.497070	139.410202	7400.535645	135.045624	7410.451660	135.072098	19725074095	7526675353

And retrieving only the Close to have something to compare.

df = df['Close']
df.head()

Symbols	BTC-USD	ETH-USD
Date
2020-01-01	7200.174316	130.802002
2020-01-02	6985.470215	127.410179
2020-01-03	7344.884277	134.171707
2020-01-04	7410.656738	135.069366
2020-01-05	7411.317383	136.276779

Let’s validate the correlation, e.g. how our values correlate to each other!

df.corr().style.background_gradient(cmap="Blues")

Symbols	BTC-USD	ETH-USD
Symbols
BTC-USD	1.000000	0.903202
ETH-USD	0.903202	1.000000

The correlation looks pretty high… We can use seaborn to show even better data by adding the plots.

import seaborn as sns

sns.pairplot(df)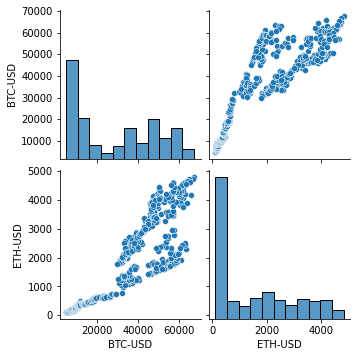

Indeed, looks very correlated! 🤩

What conclusions can we take from the above chart? Cryptocurrencies using daily data are indeed correlated, that is ETH prices depends on BTC and v.v.

This blog is getting close to its end, and as such we won’t go further in depth of this.
For the reader an excercise would be to predict the BTC price depending on ETH, which should be possible based on this correlation. We’ll go further into this later.

Data Analysis: Decomposition

Decomposing Time Series means that we try to find seasonality, trends and other things. This can be done using statsmodels which is a very impressive library that originally was done in R but now exists in Python.

from statsmodels.tsa.seasonal import seasonal_decompose

res = seasonal_decompose(df['BTC-USD'])
res.plot()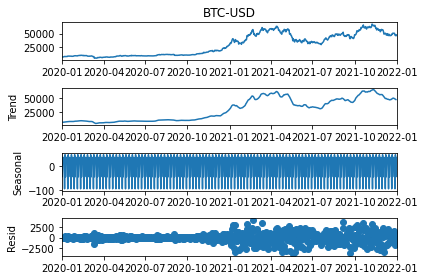

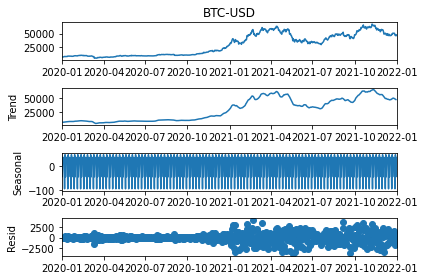
Looks nice and dandy! But we can modify this further by adding model and freq parameter to validate how it looks by decomposing either through model=multiplicative or additive, and updating the freq (period in the newest version) to decompose it based on different periods.

res = seasonal_decompose(df['BTC-USD'], model='additive', period=365) # Try weekly or monthly decomposition.
res.plot()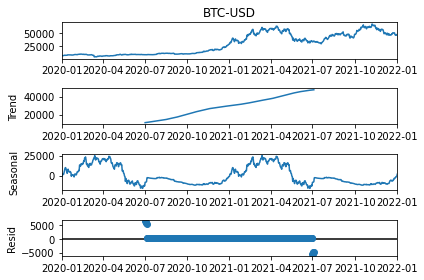

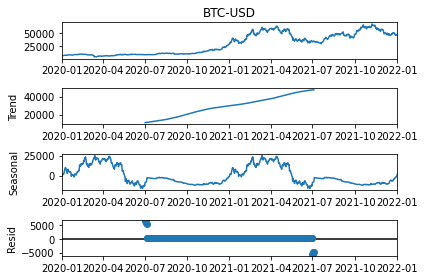
We’re now looking at our final data analysis step, Fast Fourier Transform, A.K.A. FFT!

Data Analysis: FFT

We’ll also add an Fast Fourier Transform which can show which frequencies the data “resets” at.

import numpy as np
import matplotlib.pyplot as plt

fft = np.fft.rfft(df['BTC-USD'])

plt.step(range(len(fft)), abs(fft))

plt.xscale('log')
plt.xlim([0.1, max(plt.xlim())])
plt.xticks([1, 365.2524], labels=['1/Year', '1/day'])
_ = plt.xlabel('Frequency (log scale)')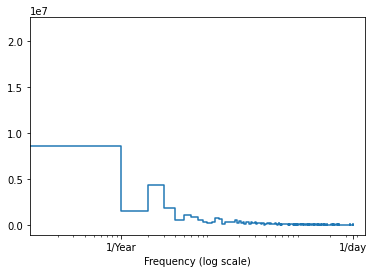

That’s it for this time. Make sure to view part 2 if you want to start predicting some data, and in part 3 we’ll do the final prediction where we’ll look at different forecast horizons!

To learn more about Time Series and how one can analyze them please view the other parts,